Модель оценки стоимости активов У. Шарпа

Банковское дело » Модель оценки стоимости активов, изгиб облигации » Модель оценки стоимости активов У. Шарпа

Уравнение является уравнением регрессии. Если его применить к широко диверсифицированному портфелю, то значения случайных переменных (εi) в силу того, что они изменяются как в положительном, так и отрицательном направлении, гасят друг друга, и величина случайной переменной для портфеля в целом стремится к нулю. Поэтому для широко диверсифицированного портфеля специфическим риском можно пренебречь, тогда модель Шарпа принимает вид:

где, Е(rр) - ожидаемая доходность портфеля; βp - бета портфеля; ур - доходность портфеля в отсутствии воздействия на него рыночных факторов.

Графически модель Шарпа представлена на рис. 1. Она показывает зависимость между доходностью рынка (rт) и доходностью актива (ri) и представляет собой прямую линию. Ее называют линией характеристики. Независимой переменной выступает доходность рынка. Наклон линии характеристики определяется коэффициентом бета, а пересечение с осью ординат — значением показателя уi.

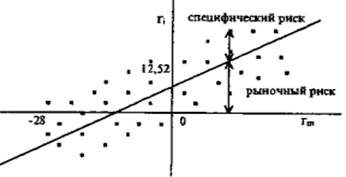
Рисунок 1 – Уравнение рыночной модели

Коэффициент бета (коэффициентом Шарпа) является – мерой инвестиционного риска финансового актива, который рассчитывается как отношения ковариации доходности актива и рыночного портфеля к дисперсии рыночного портфеля. Коэффициент бета показывает чувствительность изменения доходности актива к среднерыночной доходности. Формула связи ожидаемой доходности портфеля Е (к) и риска выраженного коэффициентом бета:

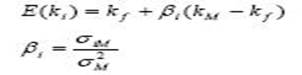
В итоге были предложены четыре основных принципа выбора портфелей:

1. Инвесторы предпочитают высокую ожидаемую доходность инвестиций и низкое стандартное отклонение. Портфели обыкновенных акций, которые обеспечивают наиболее высокую ожидаемую доходность при данном стандартном отклонении, называются эффективными портфелями.

2. Если вы хотите знать предельное влияние акции на риск портфеля, вы должны учитывать не риск акции самой по себе, а ее вклад в риск портфеля. Этот вклад зависит от чувствительности акции к изменениям стоимости портфеля.

3. Чувствительность акции к изменениям стоимости рыночного портфеля обозначается показателем бета. Следовательно, бета измеряет предельный вклад акции в риск рыночного портфеля.

4. Если инвесторы могут брать займы или предоставлять кредиты по безрисковой ставке процента, тогда им следует всегда иметь комбинацию безрисковых инвестиций и портфель обыкновенных акций.

Состав такого портфеля акций зависит только от того, как инвестор оценивает перспективы каждой акции, а не от его отношения к риску. Если инвесторы не располагают какой-либо дополнительной информацией, им следует держать такой же портфель акций, как и у других, - иначе говоря, им следует держать рыночный портфель ценных бумаг.

На рис. 1 представлен случай, когда бета положительна, и поэтому график рыночной модели направлен вправо вверх, т.е. при увеличении доходности рынка доходность актива будет повышаться, при понижении — падать. При отрицательном значении беты график направлен вправо вниз, что говорит о противоположном движении доходности рынка и актива.

Более крутой наклон графика говорит о высоком значении беты и большем риске актива, менее крутой наклон - о меньшем значении беты и меньшем риске (рис. 2). При β = 1 доходность актива соответствует доходности рынка, за исключением случайной переменной, характеризующей специфический риск. Если построить график модели для самого рыночного портфеля относительно рыночного портфеля, то значение для него равно нулю, а беты +1.

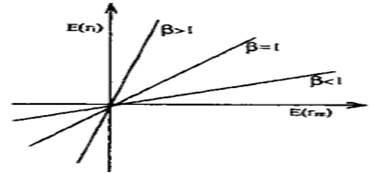
Рисунок 2 – Модель Шарпа для различных значений беты

Модель САРМ является равновесной моделью, т. е. она говорит о том, каким образом в условиях эффективного рынка устанавливаются цены финансовых активов. Модель Шарпа является индексной моделью, т. е. она показывает, каким образом доходность актива связана со значением рыночного индекса.

Теоретически САРМ предполагает рыночный портфель, и поэтому величина β в САРМ предполагает ковариацию доходности актива со всем рынком. В индексной модели учитывается только какой-либо рыночный индекс, и бета говорит о ковариации доходности актива с доходностью рыночного индекса. Поэтому теоретически β в САРМ не равна β в модели Шарпа. Однако на практике невозможно сформировать действительно рыночный портфель и таким портфелем в САРМ также выступает некоторый рыночный индекс с широкой базой. Если в САРМ и модели Шарпа используется один и тот же рыночный индекс, то β для них будет величиной одинаковой.

Еще по теме:

Объём и порядок предоставления документов
Предварительное собеседование по условиям выдачи кредита и объему документов, необходимому для рассмотрения заявки, проводится работниками кредитной службы. После предварительного собеседования для рассмотрения вопроса о выдаче кредита Заявитель предоставляет в Банк (Филиал) заявку по прилагаемой ф ...

Кредитные операции банка, их сущность и значение
Важной характеристикой экономически развитого общества является наличие эффективной системы кредитования, во многом определяющей уровень потребления. Еще в начале XIX в. граф Н. С. Мордвинов, будучи учеником Адама Смита в политической экономии, в своей работе "Рассуждения о пользах могущих пос ...

Стратегическая цель деятельности ОАО «Банк «Снежинский»
Стратегическая цель ОАО Банк «Снежинский» – выход на качественно новый уровень обслуживания клиентов, достижение позиции конкурентоспособного банка, обеспечение инвестиционной привлекательности и выход на лидирующие позиции на рынке финансовых услуг путем модернизации управленческих и технологическ ...